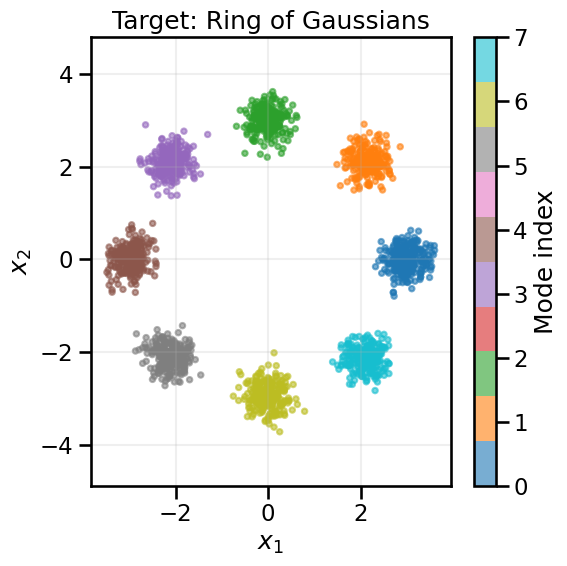
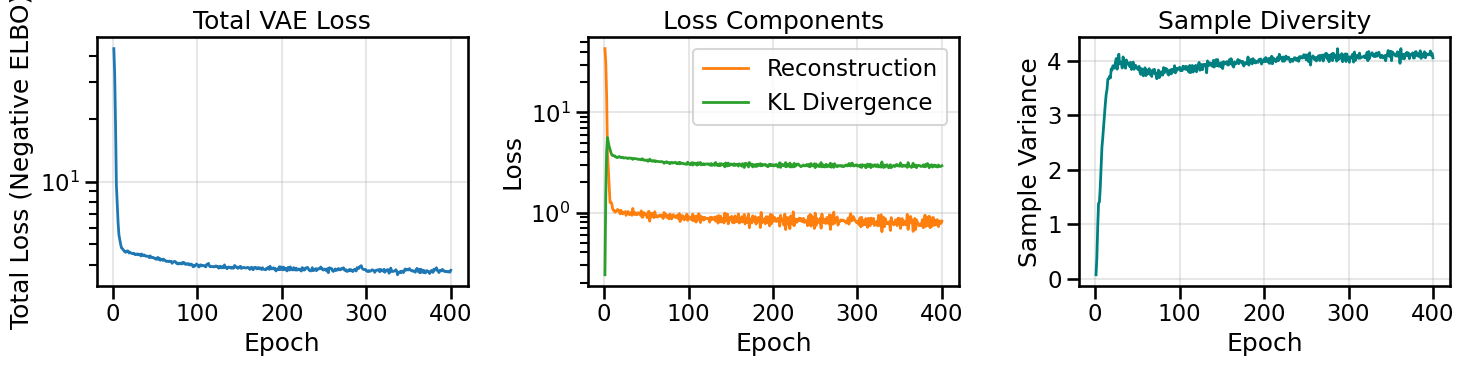
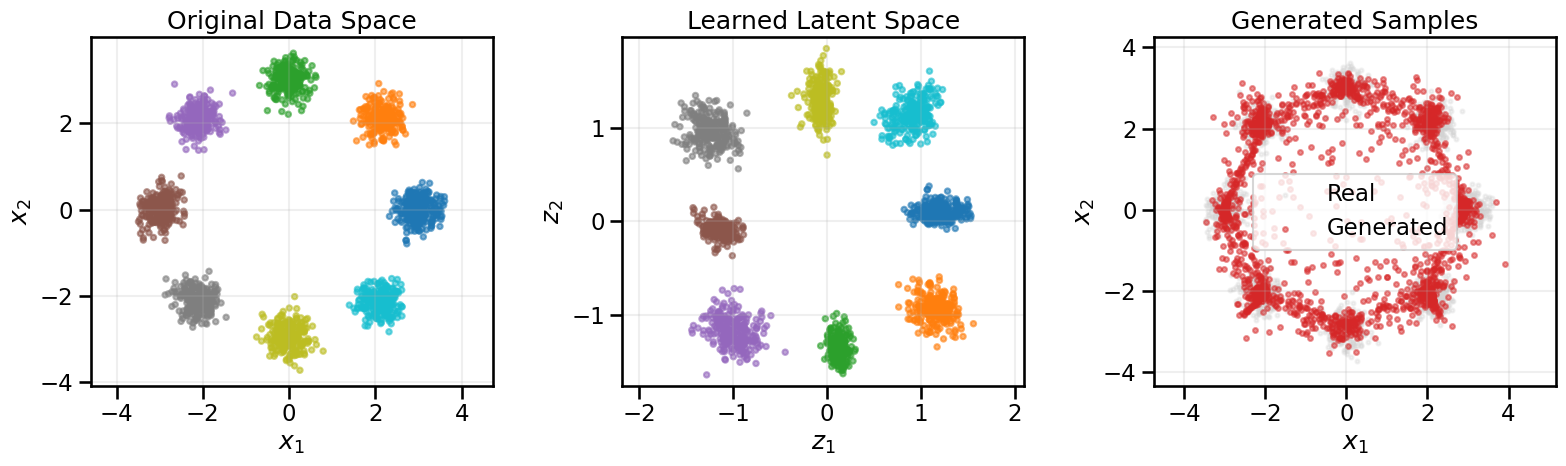
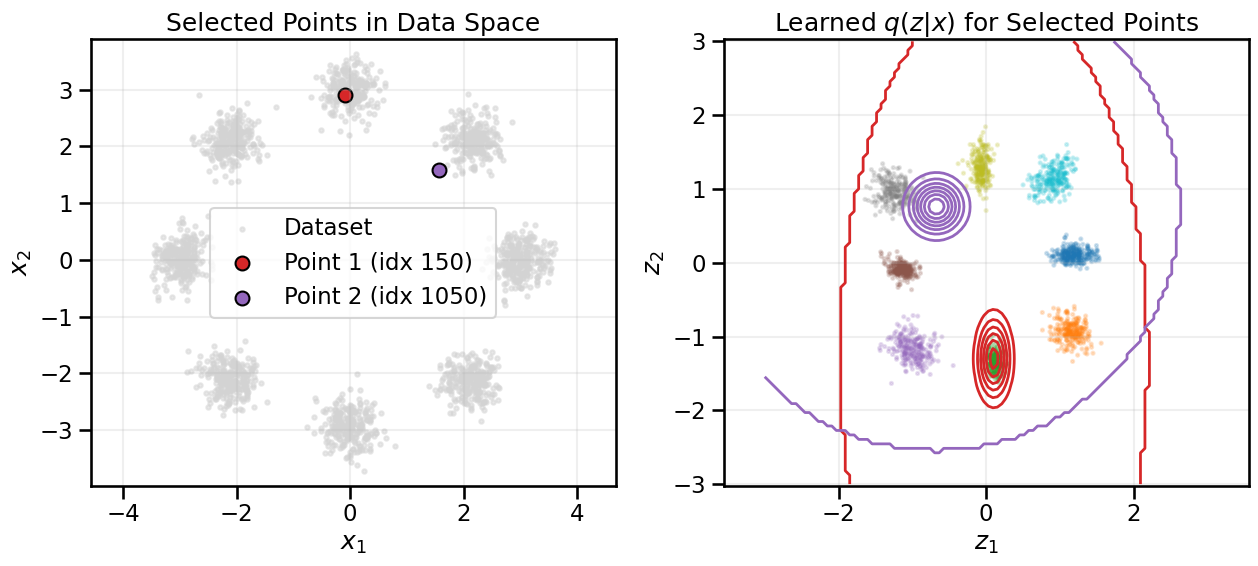
from gen_models_utilities import make_conditional_loader_radius, plot_conditional_samples_continuous
# Conditional Encoder with radius embedding
class ConditionalEncoderRadius(nn.Module):
def __init__(self, x_dim: int = 2, cond_emb_dim: int = 16, hidden_dim: int = 128, z_dim: int = 2):
super().__init__()
self.cond_embed = nn.Sequential(
nn.Linear(1, cond_emb_dim),
nn.ReLU(),
nn.Linear(cond_emb_dim, cond_emb_dim),
)
self.net = nn.Sequential(
nn.Linear(x_dim + cond_emb_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU()
)
self.mu_layer = nn.Linear(hidden_dim, z_dim)
self.logvar_layer = nn.Linear(hidden_dim, z_dim)
def forward(self, x: torch.Tensor, r: torch.Tensor):
r_emb = self.cond_embed(r)
xr = torch.cat([x, r_emb], dim=1)
h = self.net(xr)
mu = self.mu_layer(h)
logvar = self.logvar_layer(h)
return mu, logvar
# Conditional Decoder with radius embedding
class ConditionalDecoderRadius(nn.Module):
def __init__(self, z_dim: int = 2, cond_emb_dim: int = 16, hidden_dim: int = 128, x_dim: int = 2):
super().__init__()
self.cond_embed = nn.Sequential(
nn.Linear(1, cond_emb_dim),
nn.ReLU(),
nn.Linear(cond_emb_dim, cond_emb_dim),
)
self.net = nn.Sequential(
nn.Linear(z_dim + cond_emb_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, x_dim)
)
def forward(self, z: torch.Tensor, r: torch.Tensor):
r_emb = self.cond_embed(r)
zr = torch.cat([z, r_emb], dim=1)
return self.net(zr)
# Conditional VAE with radius
class ConditionalVAERadius(nn.Module):
def __init__(self, x_dim: int = 2, z_dim: int = 2, cond_emb_dim: int = 16, hidden_dim: int = 128):
super().__init__()
self.encoder = ConditionalEncoderRadius(x_dim, cond_emb_dim, hidden_dim, z_dim)
self.decoder = ConditionalDecoderRadius(z_dim, cond_emb_dim, hidden_dim, x_dim)
self.z_dim = z_dim
def reparameterize(self, mu: torch.Tensor, logvar: torch.Tensor):
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return mu + eps * std
def forward(self, x: torch.Tensor, r: torch.Tensor):
mu, logvar = self.encoder(x, r)
z = self.reparameterize(mu, logvar)
x_recon = self.decoder(z, r)
return x_recon, mu, logvar, z
def decode(self, z: torch.Tensor, r: torch.Tensor):
return self.decoder(z, r)
def train_conditional_vae_radius(
data: np.ndarray,
x_dim: int = 2, z_dim: int = 2, hidden_dim: int = 128,
batch_size: int = 256, epochs: int = 200, lr: float = 1e-3,
beta: float = 1.0, reconstruction_variance: float = 0.1, print_every: int = 50
):
loader = make_conditional_loader_radius(data, batch_size)
vae = ConditionalVAERadius(x_dim=x_dim, z_dim=z_dim, hidden_dim=hidden_dim).to(device)
optimizer = optim.Adam(vae.parameters(), lr=lr)
history = VAEHistory([], [], [], [])
for epoch in range(epochs):
total_loss, total_recon, total_kl = 0.0, 0.0, 0.0
for xb, rb in loader:
xb, rb = xb.to(device), rb.to(device)
x_recon, mu, logvar, z = vae(xb, rb)
loss, recon_loss, kl_loss = vae_loss(xb, x_recon, mu, logvar, beta, reconstruction_variance)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
total_recon += recon_loss.item()
total_kl += kl_loss.item()
with torch.no_grad():
z_sample = torch.randn(2048, z_dim, device=device)
r_sample = torch.norm(torch.randn(2048, 2), dim=1, keepdim=True).to(device)
samples = vae.decode(z_sample, r_sample)
div = compute_diversity_metric(samples)
n_batches = len(loader)
history.loss.append(total_loss / n_batches)
history.recon_loss.append(total_recon / n_batches)
history.kl_loss.append(total_kl / n_batches)
history.diversity.append(div)
if (epoch + 1) % print_every == 0 or epoch == 0:
print(f"Epoch {epoch+1:03d}/{epochs} | Loss: {history.loss[-1]:.3f} | "
f"Recon: {history.recon_loss[-1]:.3f} | KL: {history.kl_loss[-1]:.3f} | Div: {div:.3f}")
return vae, history
# Train conditional VAE with radius
cvae_radius, hist_cvae_radius = train_conditional_vae_radius(
X_ring, epochs=500, batch_size=256, lr=1e-3, beta=1.0, hidden_dim=128, z_dim=2, print_every=50
)