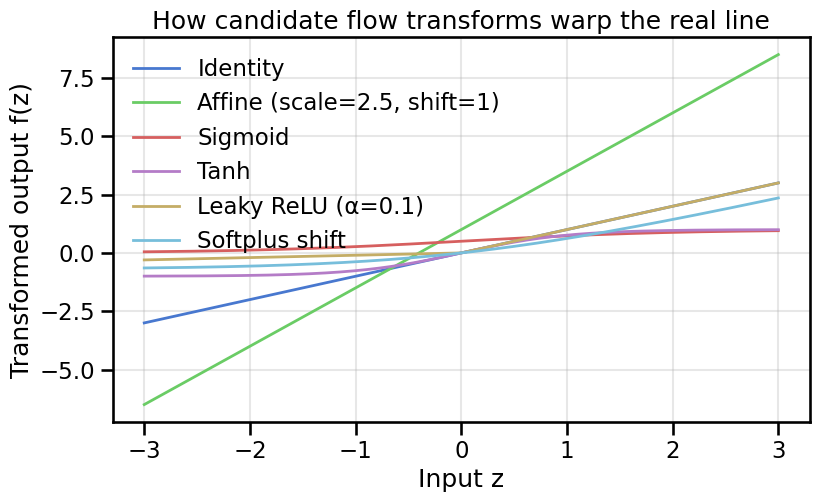
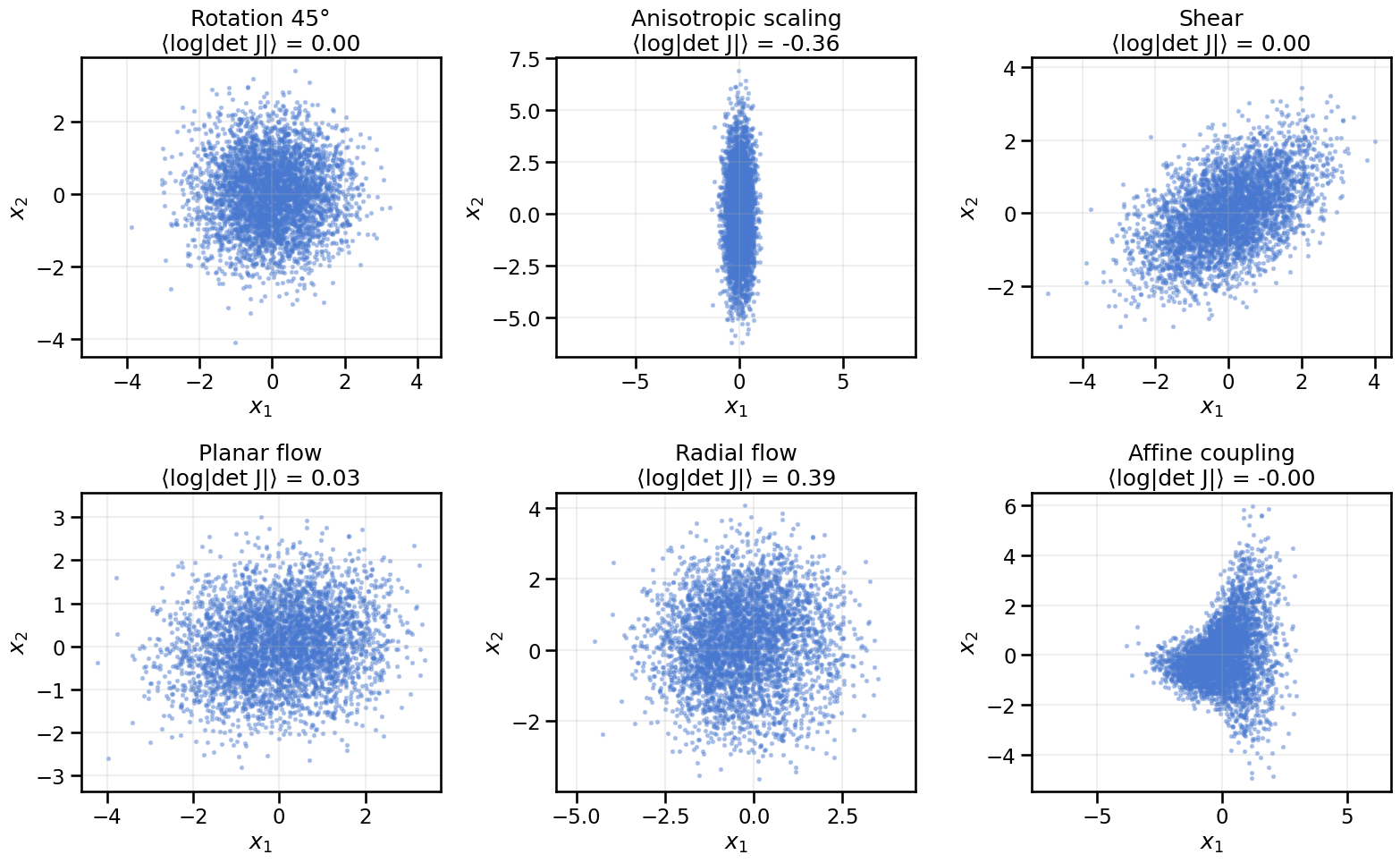
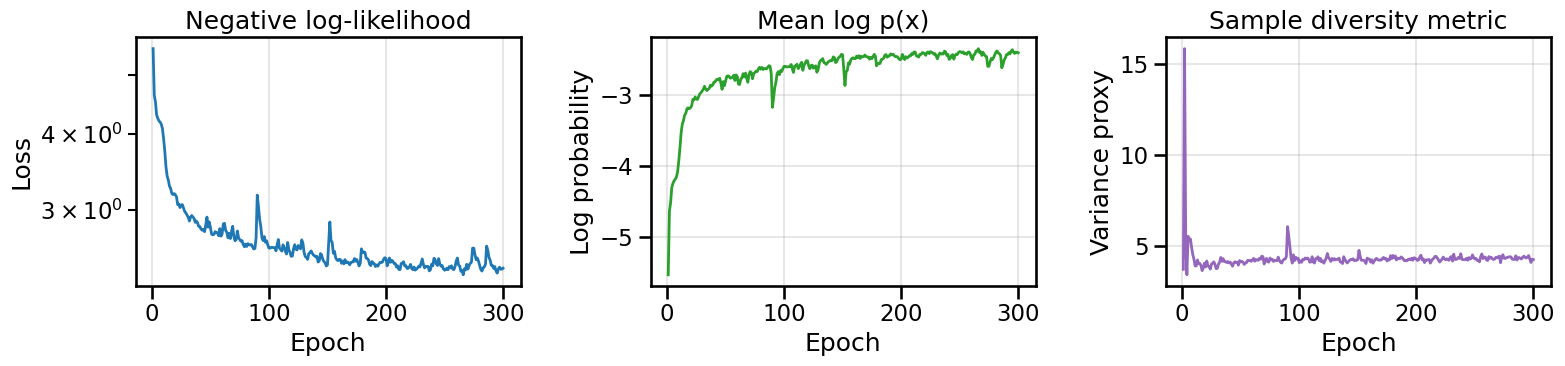
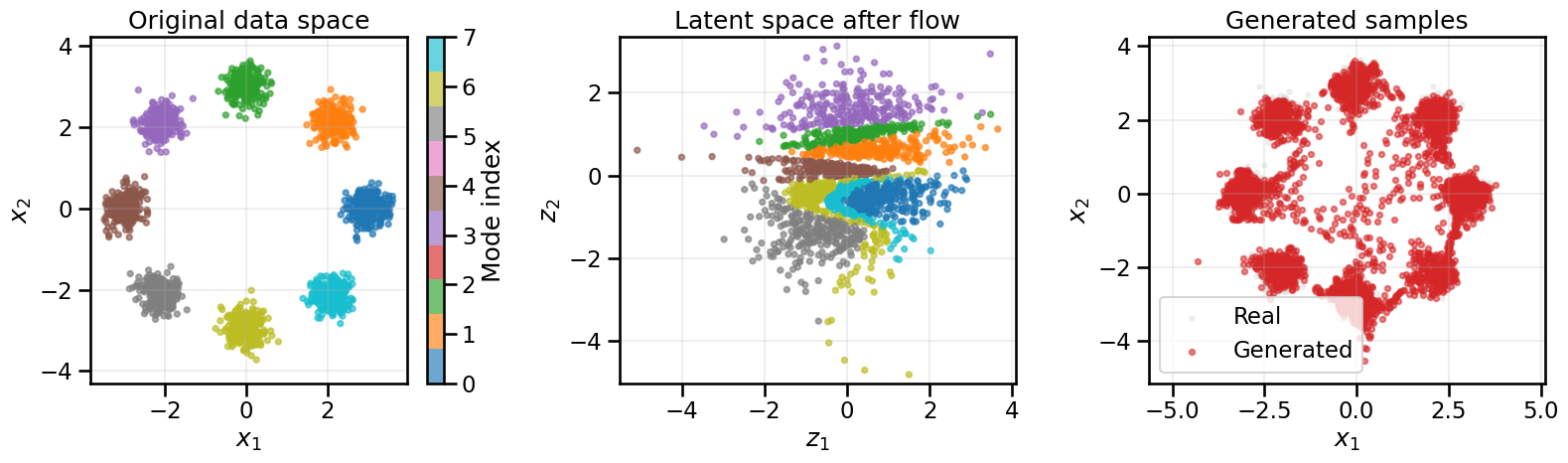
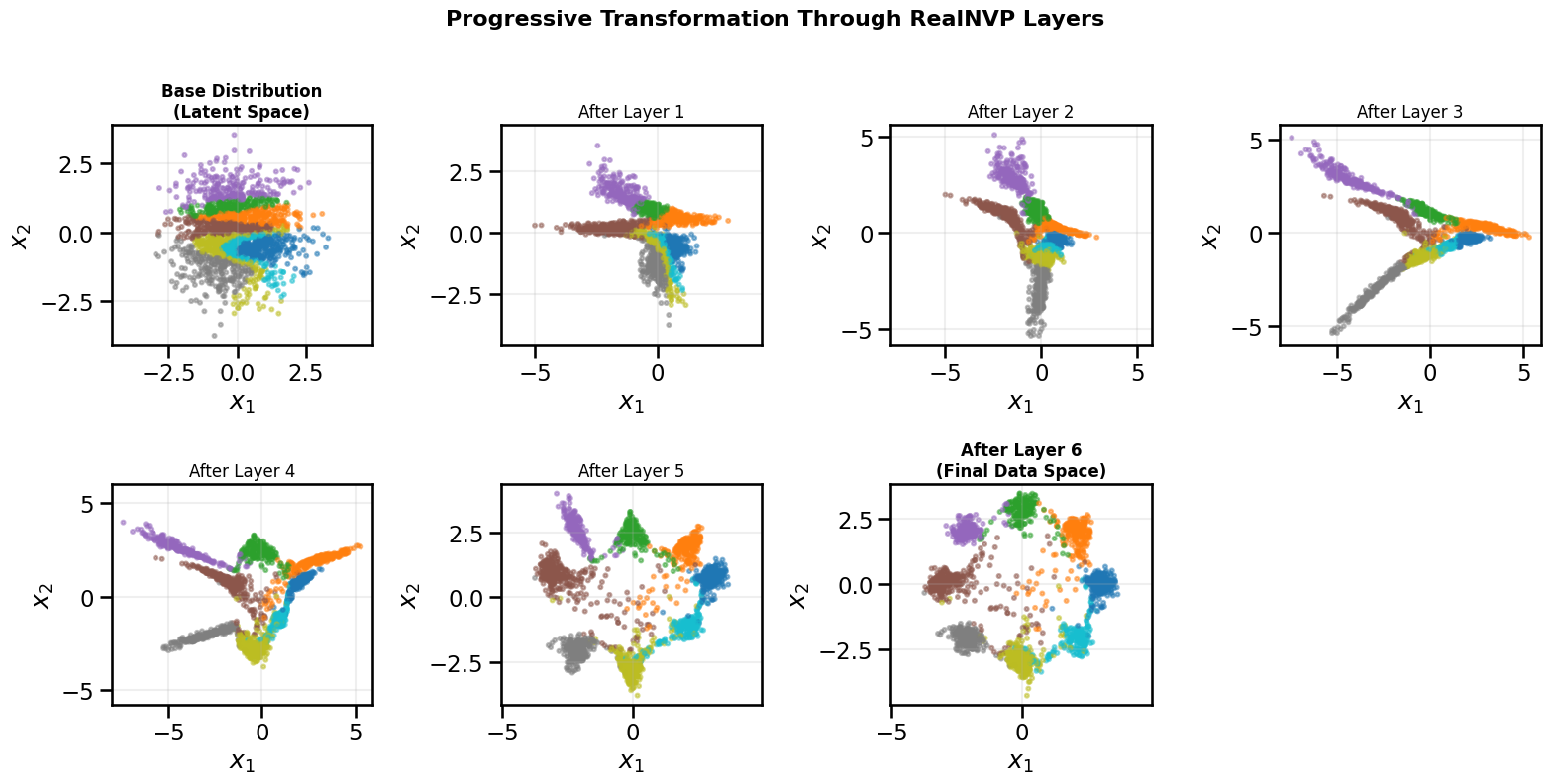
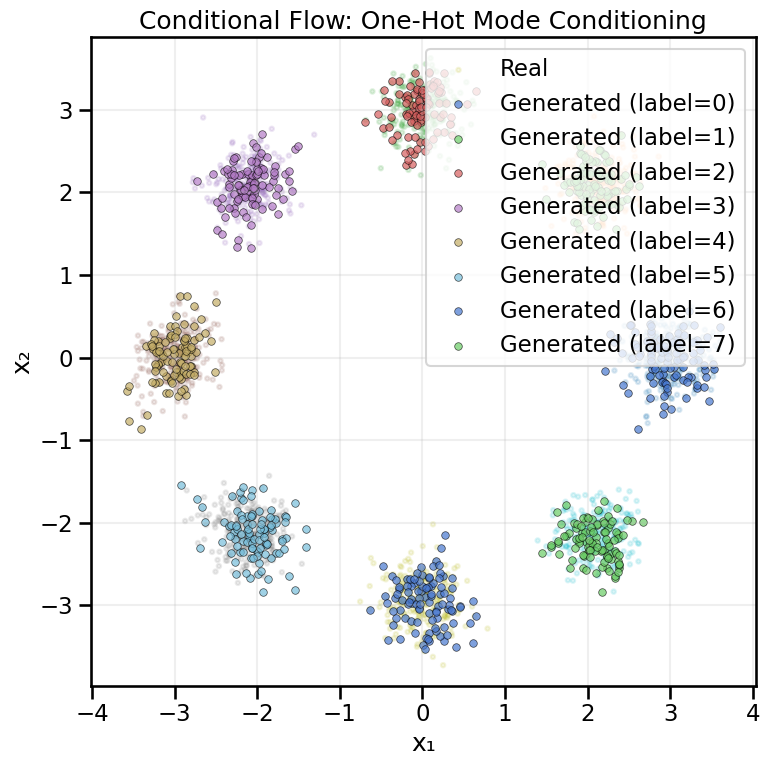
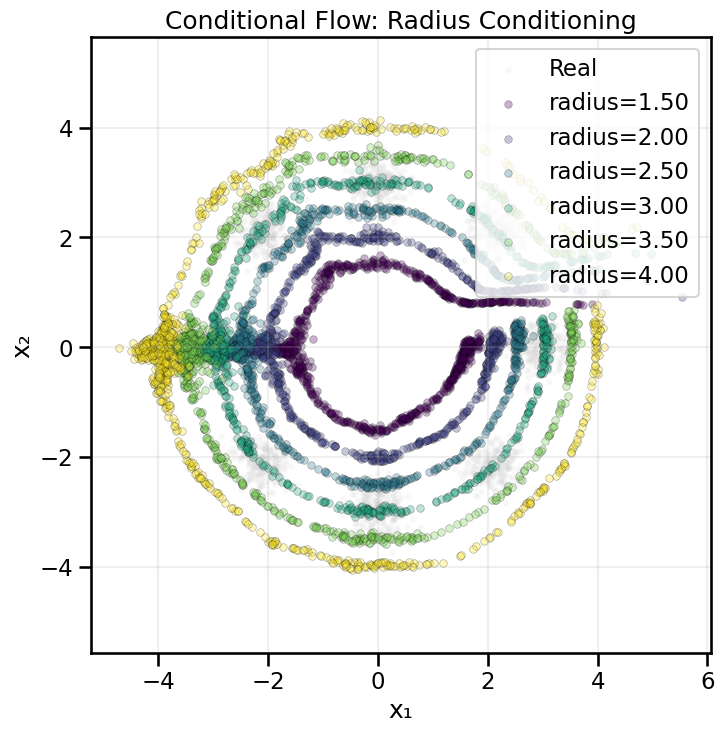
# Conditional affine coupling layer
class ConditionalAffineCoupling(nn.Module):
def __init__(self, dim: int, cond_dim: int, hidden_dim: int, mask: torch.Tensor):
super().__init__()
self.dim = dim
self.register_buffer('mask', mask)
# Condition on both masked input and label
self.scale_net = nn.Sequential(
nn.Linear(dim + cond_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, dim)
)
self.translate_net = nn.Sequential(
nn.Linear(dim + cond_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, dim)
)
nn.init.zeros_(self.scale_net[-1].weight)
nn.init.zeros_(self.scale_net[-1].bias)
nn.init.zeros_(self.translate_net[-1].weight)
nn.init.zeros_(self.translate_net[-1].bias)
def forward(self, x: torch.Tensor, y: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
x_masked = x * self.mask
xy = torch.cat([x_masked, y], dim=1)
s = self.scale_net(xy) * (1 - self.mask)
t = self.translate_net(xy) * (1 - self.mask)
s = torch.tanh(s)
out = x_masked + (1 - self.mask) * (x * torch.exp(s) + t)
log_det = ((1 - self.mask) * s).sum(dim=1)
return out, log_det
def inverse(self, y_out: torch.Tensor, y_cond: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
y_masked = y_out * self.mask
yc = torch.cat([y_masked, y_cond], dim=1)
s = self.scale_net(yc) * (1 - self.mask)
t = self.translate_net(yc) * (1 - self.mask)
s = torch.tanh(s)
x = y_masked + (1 - self.mask) * ((y_out - t) * torch.exp(-s))
log_det = -((1 - self.mask) * s).sum(dim=1)
return x, log_det
# Conditional RealNVP
class ConditionalRealNVP(nn.Module):
def __init__(self, dim: int = 2, cond_dim: int = 8, hidden_dim: int = 128, n_layers: int = 6):
super().__init__()
masks = []
for i in range(n_layers):
mask = torch.tensor([1.0, 0.0]) if i % 2 == 0 else torch.tensor([0.0, 1.0])
masks.append(mask)
self.layers = nn.ModuleList([
ConditionalAffineCoupling(dim=dim, cond_dim=cond_dim, hidden_dim=hidden_dim, mask=mask)
for mask in masks
])
def forward(self, x: torch.Tensor, y: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
log_det_total = torch.zeros(x.shape[0], device=x.device)
z = x
for layer in self.layers:
z, log_det = layer(z, y)
log_det_total = log_det_total + log_det
return z, log_det_total
def inverse(self, z: torch.Tensor, y: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
log_det_total = torch.zeros(z.shape[0], device=z.device)
x = z
for layer in reversed(self.layers):
x, log_det = layer.inverse(x, y)
log_det_total = log_det_total + log_det
return x, log_det_total
def log_prob(self, x: torch.Tensor, y: torch.Tensor, base_dist: MultivariateNormal) -> torch.Tensor:
z, log_det = self.forward(x, y)
log_prob_base = base_dist.log_prob(z)
return log_prob_base + log_det
def sample(self, y: torch.Tensor, base_dist: MultivariateNormal) -> torch.Tensor:
with torch.no_grad():
z = base_dist.sample((y.shape[0],))
x, _ = self.inverse(z, y)
return x
def train_conditional_flow_onehot(
data: np.ndarray, labels: np.ndarray, n_classes: int = 8,
epochs: int = 300, batch_size: int = 256, lr: float = 1e-3, print_every: int = 50
):
loader = make_conditional_loader_onehot(data, labels, batch_size, n_classes)
flow = ConditionalRealNVP(dim=2, cond_dim=n_classes, hidden_dim=128, n_layers=6).to(device)
base_dist = MultivariateNormal(
loc=torch.zeros(2, device=device),
covariance_matrix=torch.eye(2, device=device)
)
optimizer = optim.Adam(flow.parameters(), lr=lr)
history = FlowHistory(loss=[], log_prob=[], diversity=[])
for epoch in range(epochs):
batch_losses, batch_log_probs = [], []
for xb, yb in loader:
xb, yb = xb.to(device), yb.to(device)
log_prob = flow.log_prob(xb, yb, base_dist)
loss = -log_prob.mean()
optimizer.zero_grad()
loss.backward()
optimizer.step()
batch_losses.append(loss.item())
batch_log_probs.append(log_prob.mean().item())
with torch.no_grad():
y_sample = torch.nn.functional.one_hot(
torch.randint(0, n_classes, (2048,), device=device), num_classes=n_classes
).to(torch.float32)
samples = flow.sample(y_sample, base_dist)
diversity = compute_diversity_metric(samples)
history.loss.append(float(np.mean(batch_losses)))
history.log_prob.append(float(np.mean(batch_log_probs)))
history.diversity.append(diversity)
if (epoch + 1) % print_every == 0 or epoch == 0:
print(f'Epoch {epoch + 1:03d}/{epochs} | Loss: {history.loss[-1]:.3f} | '
f'Log p(x|y): {history.log_prob[-1]:.3f} | Div: {diversity:.3f}')
flow.eval()
return flow, base_dist, history
# Train conditional flow
cflow_onehot, cflow_base_dist, cflow_hist_onehot = train_conditional_flow_onehot(
X_ring, y_ring, n_classes=8, epochs=300, batch_size=256, lr=1e-3, print_every=50
)